
如何对人力资源进行优化配置,是很多HR从业者需要面临的问题,案例中是要运用一定手段在保持利润最大化的情况下进行人力资源优化配置,EXCEL的线性规划求解正好可以解决这个问题。
—————————————————————————————————————————————
本课内容取自:三茅专栏作家、打卡牛人齐涛 2015-3-24 发表的打卡总结《用EXCEL规划求解工具进行人力资源优化配置》
—————————————————————————————————————————————
案例:
A公司确定2015年的目标是主推五种产品,其中产品1、产品2、产品3三种产品全年销售额不能低于总销售额的15%、30%、20%,产品5全年销售额不能高于总销售额的10%,继续保持推出科技含量高的新产品引领市场。生产单位产品各工段需求人数、每个工段现有人数、最大用工量及每个产品的利润如下表,公司生产员工总共300人,假如你是人力资源经理,在保持公司利润最大化的情况下如何实现人力资源的优化配置?
|
产品 工段 |
产品1 |
产品2 |
产品3 |
产品4 |
产品5 |
现有人数 |
最大用工量 |
|
工段1 |
26 |
24 |
23 |
18 |
16 |
53 |
65 |
|
工段2 |
20 |
15 |
10 |
30 |
6 |
60 |
60 |
|
工段3 |
35 |
31 |
20 |
22 |
23 |
65 |
80 |
|
工段4 |
30 |
27 |
28 |
9 |
25 |
63 |
70 |
|
工段5 |
19 |
26 |
35 |
18 |
10 |
59 |
100 |
|
利润(万元) |
3.3 |
1.9 |
2.85 |
2.3 |
1.7 |
- |
- |
案例解析:
如何对人力资源进行优化配置,是很多HR从业者需要面临的问题,案例中是要运用一定手段在保持利润最大化的情况下进行人力资源优化配置,EXCEL的线性规划求解正好可以解决这个问题。
一、设定决策变量
通过案例我们发现五种产品的单位产量是变量,设产品1、产品2、产品3、产品4、产品5的单位产量分别为X1、 X2 、X3 、X4、 X5。
二、设定目标函数
案例中是要在利润最大化的情况下进行人力资源优化配置,所以目标函数为利润最大化。设总利润为Z,则目标函数为:
MAX Z=3.3 X1+1.9 X2+2.85X3+2.3X4+1.7X5
三、设定约束条件函数
约束条件是为指实现系统目标的限制因素。在本案例中,每个工序都有最大人数的限制,并且产品1、产品2、产品3和产品5有销售比例的限制。
根据工段1最大人数的限制,得到约束条件函数:
26 X1+24X2+23X3+18X4+16X5<=65 (1)
同理,根据工段2、工段3、工段4和工段5最大人数的限制,得到约束条件函数:
20X1+15X2+10X3+30X4+6X5 <=60 (2)
35X1+31X2+20X3+22X4+23X5<=80 (3)
30 X1+27X2+28X3+9X4+25X5 <=70 (4)
19 X1+26X2+35X3+18X4+10X5 <=100 (5)
根据产品1、产品2、产品3和产品5有销售比例的限制,得到约束条件函数:
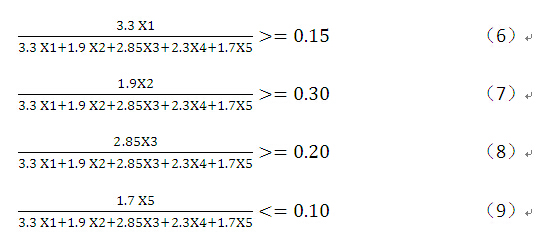
同时,X1、 X2 、X3 、X4、 X5应该为非负数,得到约束条件函数:
X1>=0,X2>=0,X3>=0,X4>=0, X5>=0 (10)
经过简化变形上述约束条件函数,得到约束条件函数:

四、建立模型并求解
(一)模型建立
根据上述目标函数和约束条件函数,在EXCEL上建立模型。如图1。
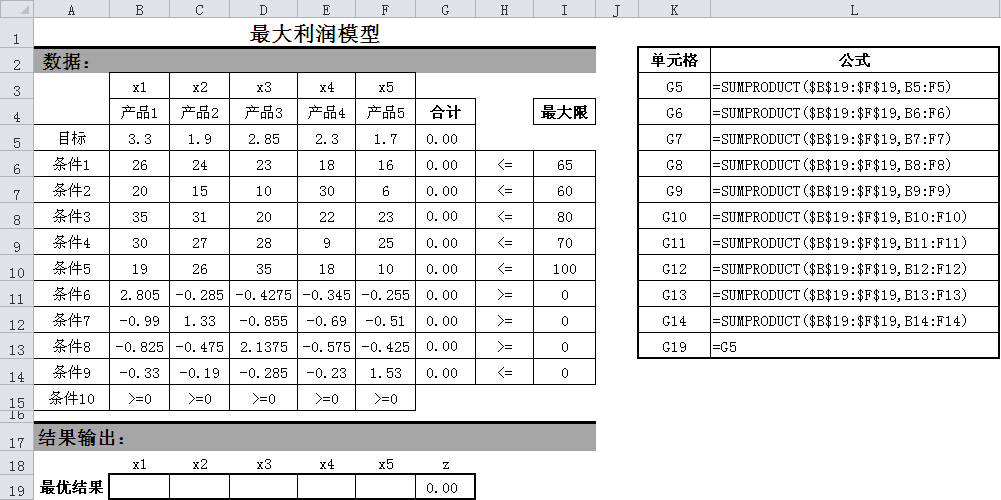
图1 最大利润模型
(二)参数设置
利用EXCEL上的规划求解工具,对各参数进行设置。如图2。
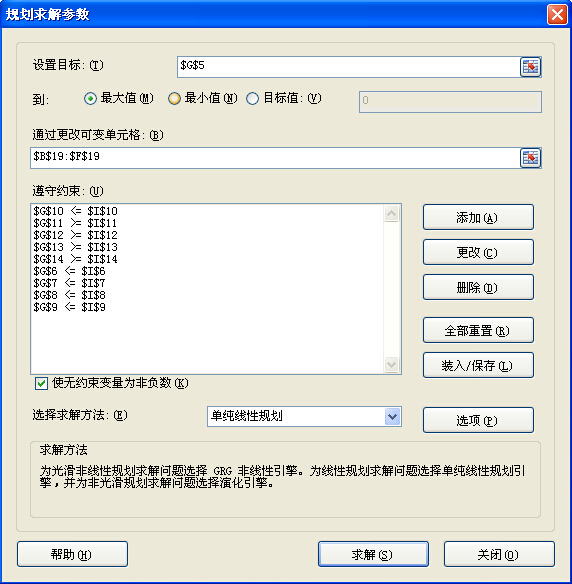
图2 参数设置
(三)求解
运行求解后得到求解结果如图3所示。
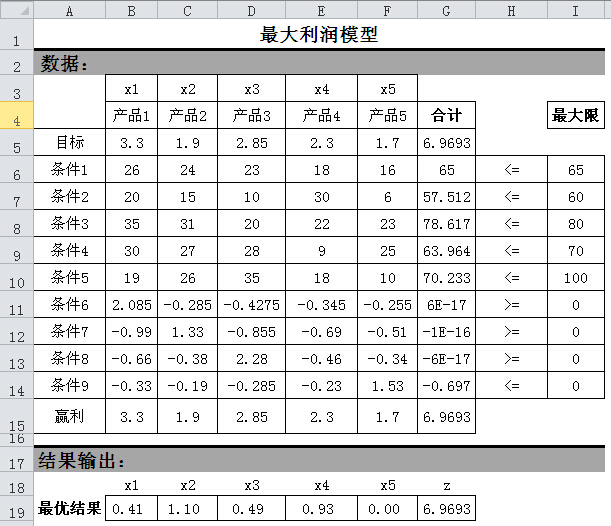
图3 规划求解结果
五、规划求解结果分析
根据图3的结果,我们可以看出企业要实现利润最大化,五种产品的产量分别如图中最优结果所示。因为本模型计算的是单位产量下利润最大化,所以最优结果出现小数是允许存在的。
案例中是要保持公司利润最大化的情况下如何实现人力资源的优化配置,图3中可以看出各工段最小需求人数,我们可以建立一个表格更直观的看到结果,如图4。
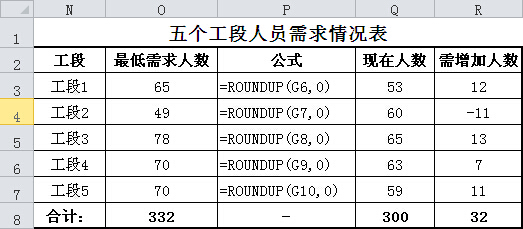
图4 人员需求情况表
根据图4可以看到,在保持利润最大化的情况下公司生产人员是欠缺的,需要再增加32人。分析各工段人员需求情况我们还会发现工段2的人员是富余的,需要调整11人到其它工段。
六、结论
上述情况是根据最优结果得出的人员需求情况,总体需要招聘,1个工段人员需要调整。我们建立的模型是计算得出最优的结果,但是市场经济下,企业的行为受市场经济调控,企业不可能完全按最优结果生产和销售其产品,而且技术工艺的改进、人员出勤率等影响,生产人员的优化配置会和模型计算的结果有偏差,但通过线性规划求解,为案例中的人力资源经理提供了人员配置的最优结果,为他的人员配置提供了依据。如果有更多的约束条件,我们可以得出更趋向于实际的结果。




